女儿问了我一道小学六年级的数学题,题目如下:

找规律的数学题,题目看着很简单,不过我没作出来,脑子只发育到了每增加一层,增加层的正方体数量是上一层数量加 4,至于是什么规律,用数学表达式我搞不出来。
当时第一时间想到一个脑子聪明伶俐的女朋友,后来想想,还是问问 AI 吧,因为无法上传图片识别,所以我把题目改成了“1 6 15 28 ... 根据数字规律列出数列通用式子,并计算第10位数字”。
然后一道小学数学题被 AI 作出高中数学的感觉,答案还各不相同,看着都不怎么靠谱,本来就不会,被一解释更不会了。下面是各个 AI 的答案:
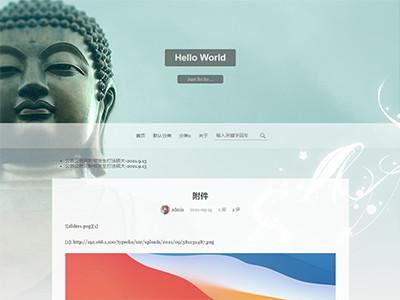
1. 阿里云百练(原来好像是通义千问,居然还有免费次数限制了)

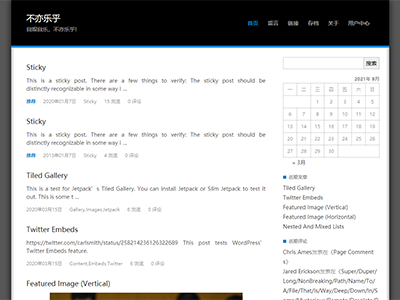
2. 讯飞星火(这个感觉靠谱点)

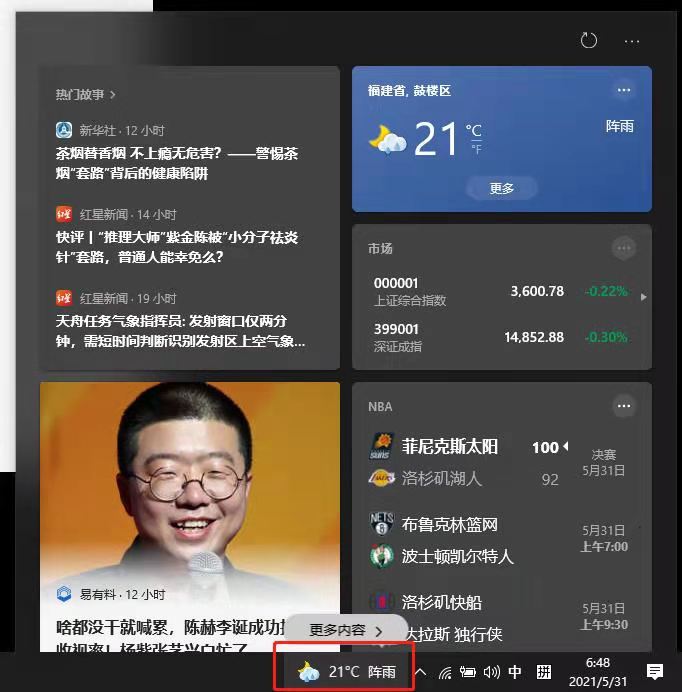
3. 天工大模型

4. Kimi (这纯粹自由发挥)

THE END




1
1+4x1
1+4x2
。
。
1+4x(n-1)
求和:1xn+4x[1+2+...+(n-1)]=n+2n(n-1)
木木老师一向都是这么高效简洁
哈,已经在小学误人子弟十多年啦~这题5年级学过等差数列求和公式就可以做啦(首项+末项……)
木木老师太谦虚了,原来你还是教数学的,还以为是坐办公室的,像教务处什么的。
降维打击啊。。。
思考过程如下:
通过题目描述,已知条件:
| 层数 | 中间方块 | 边缘方块 | 每层方块总数 |
| ---- | -------- | ------- | --------- |
| 1层 | 1 | 0 | 1 |
| 2层 | 1 | 4 | 5 |
| 3层 | 1 | 8 | 9 |
要计算方块总和,拆分问题成2个问题:
1.计算中间方块数量总和
2.计算4边方块数量总和(以下称「边缘方块」)
总和 = 中间方块数量总和 + 边缘方块数量总和
中间方块计算公式:
中间的方块,每一层都是1个,第1层有1个,第2层有2个,......所以推导出第n层有n个
所以中间的方块可以得出公式:n*1
边缘方块计算公式:
先推倒出每一层的边缘方块数量计算公式
观察上面边缘方块变化得知,每一层有4个边(看图示),每边的方块数量随层数递增4个
注:第3层是从题目得知3层共有方块15个,那么第3层数量 = 15-第1层方块数量-第2层方块数量,得到9个,减去中间1个,除4,得到每边数量
第1层,每边0个(0*4 = 0个)
第2层,每边1个(1*4 = 4个)
第3层,每边2个(2*4 = 8个)
可以推算出每层的边缘方块数量是:(层数-1)*4,即(n-1)*4
而上面说到每一层的数量是递增4个,也就是每层之间的差是4个
将方块总数的数据排列出来,可以发现每一层的总数排列起来实际上是一个等差数列:0、4、8、12、16、20
(以下通过边缘方块数量计算公式,(n-1)*4推算)
第1层,每边0个(0*4 = 0个)
第2层,每边1个(1*4 = 4个)
第3层,每边2个(2*4 = 8个)
第4层,每边3个(3*4 = 12个)
第5层,每边4个(4*4 = 16个)
第6层,每边5个(5*4 = 20个)
那么可以直接套等差列求和公式:项数*(首项+尾项)/2
首项:4(因为第1层没有方块,从第2层开始算)
尾项:(n-1)*4,可以简写为4(n-1)
项数: n-1(因为从第2层开始计算)。
尝试验证:
验证第1-3层的边缘方块总和,等差数列为0、4、8
第1层,(1-1)*4 = 0个
第2层,(2-1)*4 = 4个
第3层,(3-1)*4 = 8个
套公式:
=(3-1)*(4+8)/2
= 2*12/2
= 24/2
=12(正确)
验证第1-5层的边缘方块总和,等差数列为0、4、8、12、16
第1层,(1-1)*4 = 0个
第2层,(2-1)*4 = 4个
第3层,(3-1)*4 = 8个
第4层,(4-1)*4 = 12个
第5层,(5-1)*4 = 16个
套公式:
=(5-1)*(4+16)/2
=4*20/2
=80/2
=40(正确)
然后将两者加起来即可(中间方块数量总和 + 边缘方块数量总和),假设层数为n
通用公式如下:
方块总和= n*1 +( 4+4(n-1) )/2*n-1
尝试验证:
第1层:
1*1 +(-4+ 4)/2*0
= 1 + 0
= 1(正确)
第1层+第2层:
2*1 + (4+4)/2 *1
= 2 +4 = 6
= 6(正确)
第1层+第2层+第3层:
3*1 + (4+8)/2*2
= 3+12
= 15(正确)
....
用心了,不过一道小学数学题被你解出大学高等数学的感觉,不知道是小学疯了还是我疯了。
hhhh,现在的小学生、初中生做的题太难了,数学早忘的一干二净了,现在大了回看他们写公式,感觉在看天书一样,完全看不懂
想起网上说的一句,中考高考是人生智力的巅峰.......
用了一段时间的kimi,他的模式就是搜索+总结
我娃要是碰到这种题来问我我是教不了
这题目是培养孩子空间概念的。
反正我看这题的时候脑子里就在搭积木。
我认为AI的解法都是超纲的。
其实按照小学的算数,应该是
1=1
1+[(1)x4+1]=6
6+[(2)x4+1]=15
15+[(3)x4+1]=28
……
你这个和我想的一样,都是在上一个层的基础上加,算第十层要先算前面的9层。
极度同意。
N级台阶最中间就需要 N 块积木,然后 4 个方向每边由中心 N 递减至 1,由此计算需要的总积木为 4*[1+2+3+…+(N-1)]+N
你这个思路没错,但结果错了。中间方块合计是n,第二层开始边上都是4个方块往外扩张,每一层都增加 4(n–1),总方块应该是 n+∑4(n–1)。
没错吧,式子化简后是 N*(2N-1)
有道理。
对了,你博客的twikoo评论是不是有问题,无法提交。
哈哈,薛定谔的评论,现在应该 OK 了。
自己搭建的服务器应该不至于吧,难道是我这边网络原因。
这些ai都不如姐姐我
应该是n+2*n*(n-1)
还是姐姐你厉害,来,娃给你教。